Understanding S-Parameter Causality in ADS for Signal and Power Integrity
- Tyler Huddleston
- Aug 7, 2025
- 15 min read
Updated: Sep 16, 2025
When we teach about S-parameters and modeling, someone never fails to ask “What is causality?” or “What happens if a model isn’t causal?” Our go-to explanation is that it's a cause and effect thing: a system is causal if its output doesn’t respond before its input changes. In a causal universe, the light shouldn't turn on before you flip the switch.
This seems straightforward. After all, if you're modeling or measuring a physical system — say, interconnects between a driver and receiver — shouldn't the result naturally be causal?
Like most things in engineering, the answer is not always. In this post, we’ll explore:
How non-causal S-parameters can result from real measurements or simulations
How to detect and visualize causality violations
The consequences of using a non-causal model in time-domain simulation
And how to avoid generating or using non-causal data
What is Causality?
Causality describes the relation between cause and effect in system behavior, emphasizing how outputs are connected to prior inputs. In a Signals & Systems course, we study linear-time invariant (LTI) systems because they follow predictable rules and closely model many physical systems. Circuits, filters, and communications channels are typically LTI or can be approximated as such over a limited range of operating conditions.
Crucially, the mathematics of LTI systems is nicely structured: convolution in time becomes multiplication in frequency, eigenfunctions are sinusoids, and powerful tools like Fourier and Laplace transforms only apply under the assumptions of linearity and time invariance. The assumption of linearity and time invariance is important for these mathematical techniques to be valid and for the analysis to be accurate.
One key criterion for a system to be LTI is causality.
A system is causal if its impulse response is zero for all times before the impulse is applied. In other words, a causal system’s output at any given moment depends only on past and present inputs — never future ones.
The impulse response, h(t), is the output of a system when the input is a Dirac delta function, δ(t), applied at t = 0. The mathematical form of the impulse response, typically expressed as h(t), is fundamental in analyzing system behavior and determining properties like causality. To test for causality, we examine h(t): the system is causal if h(t) = 0 for all t < 0.
In simpler terms, if an input stimulus is applied to a system and if any part of the output arrives in time before the input, then the system is non-causal.
When analyzing LTI systems, eigenfunctions and their corresponding eigenvalues are responsible for defining the system's response. Functions such as exponentials and sinusoids are used to represent inputs and outputs, highlighting how functions are integral to describing and understanding system behavior.
How can sampling in the frequency domain affect time-domain simulation?
System characterization is typically done in the frequency domain. For example, a Vector Network Analyzer (VNA) applies a sine wave stimulus at one port and measures the response at all ports. By sweeping the frequency of the input signal and recording the resulting behavior, the VNA builds a picture of how the system responds across a defined frequency range. These measurements are commonly saved in an S-parameter file, which can then be directly used by most circuit simulators as a system model.
Hybrid solvers like SIPro or full 3D solvers like RFPro operate similarly: they solve Maxwell's equations in the frequency domain and return a dataset that characterizes system behavior across frequency. The result can also be exported as an S-parameter model.
With such a model, any arbitrary time-domain input — like a pulse, step, clock, FM, or digital waveform — can be applied. The simulator will compute the corresponding output using inverse Fourier techniques. This process involves a specific technique to convert frequency-domain data to the time domain, ensuring the time-domain response accurately reflects the original system.
But if the real world operates in the time-domain, why bother with the frequency domain to begin with? To quote the self-proclaimed (and who could argue?) Signal Integrity Evangelist Eric Bogatin: "We go to another domain when it's easier to get the answer there." [1]
The frequency domain is preferred both in hardware and computation because it's faster and more practical to measure most linear systems this way. Time-domain measurements require a very high bandwidth and sampling rates. A time-domain reflectometer (TDR) or oscilloscope must capture very fast edges with high dynamic range, which becomes expensive and technically challenging at multi-gigahertz speeds. In contrast, frequency-domain measurements can average over many cycles of a sine wave at each point, reducing noise and improving dynamic range. It's also much easier to precisely control the frequency content, impedance, and power level with a VNA — something far harder to do in the time domain.
In fact, even full-wave EM solvers like SIPro and RFPro typically solve systems in the frequency domain. This is because Maxwell's equations, though inherently time-dependent, become much simpler when solved for steady-state sinusoidal excitation. Time derivatives convert to multiplications, reducing the problem to a linear algebraic system at each frequency point. This is often computationally cheaper and more stable than time-domain solvers, especially when high-frequency accuracy and broadband behavior are needed.
However, the system models created in the frequency domain by these methods are inherently discrete and bandwidth-limited. That is, the system isn’t fully defined over the entire frequency continuum, but only at a set of sampled points. The density and range of this set directly correlates to the accuracy of the model in both the frequency and time domains.
The discrete frequency data must be converted to a time-domain representation to simulate behavior in the time domain. With any conversion of a finite set however, something is always at risk of being lost or distorted in the translation.
If the frequency sampling is too sparse, too narrow in bandwidth, or lacks proper phase continuity, the resulting time-domain model may no longer reflect the true behavior of the original physical system—and in some cases violate physics altogether.
How can you check for causality violations?

If Miss Minutes (from Marvel’s TVA) isn’t available to flag time-travel violations in your simulation, you can still check causality the normal way — with Keysight ADS.
To illustrate how a non-causal S-parameter model can arise, I set up a simple channel simulation experiment using three system representations of the same structure:
An ideal transmission line model
A causal S-parameter model, created using a dense frequency sweep
A non-causal S-parameter model, generated by undersampling the frequency response
All three models represent the same 1-inch 50Ω lossy transmission line. The baseline model is the built-in TLINP component in ADS using all of the default parameters, which produce a line delay of 123 ps.
The causal and non-causal models were created by sweeping the transmission line's S-parameters from 1 MHz to 35 GHz — once with high frequency resolution of 1000 evenly spaced linear samples and once with low resolution at 5 linear samples. The simulation schematic is shown in Figure 1.

The results of the under-sampled and adequately-sampled S-parameter simulations are shown below in Figure 2. The 5 under-sampled points are placed at the circles on the red plot with a linear interpolation connecting the points. By under-sampling, we exclude many of the dynamic characteristics of the transmission line as made evident by the error from the under-sampled plot to the well-sampled one.

I exported the results to S-parameter files using the Data File Tool from the DDS window.
To verify the models are indeed non-causal and causal as intended, I checked them in ADS's S-Parameter Toolkit, which can be opened from a schematic window under Tools > Data File Utilities ... > S-Parameter Toolkit, or by placing an SnP component on the schematic, assigning the s-parameter file, and clicking the Check/View S-Parameters button.
The S-Parameter Toolkit checks causality by analyzing the underlying mathematical equation and the specific forms of the S-parameter data, ensuring that the frequency response is consistent with physical system behavior. See the S-Parameter Toolkit documentation at "Verifying S-Parameter Data" page in the built-in ADS documentation under Help > Topics and Index ... for plenty of details on how to use it. We have a list of great ADS Learning and Training Resources for plenty of reference on how to setup and run simulations like those shown in this post.
The causality results of the non-causal model are shown first below in Figure 3. Note the information provided in the Summary section. It tells us the model's bandwidth is 1 MHz to 35 GHz, that there are 5 points, and that the reference impedance is 50Ω as expected. Reciprocity (for example, whether through ports are reciprocal, as in S21 = S12) and passivity (if the model is passive, as in it stores or dissipates energy and does not create it) are calculated by default when loading the file. Causality can be checked by clicking the Causality tab and then the Start Calculation button.
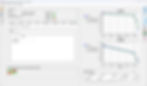
When a model is non-causal, the failing S-parameters in the matrix selector are colored red. The failing S12 parameter is selected as an example. The real and imaginary causality factors are plotted in blue, with the allowed range plotted between the dotted green lines. Note that the non-causal points all fall outside the green limit lines.
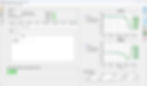
Conversely, all points of the causal model are within the causal limits as seen in Figure 4.
What are the Consequences of Using a Non-Causal Model?
Now that we've got an ideal model, a causal s-parameter model, and a non-causal s-parameter model, let's observe how they compare in the time domain. When comparing these models, we are essentially analyzing the response of a system to a given input, where the transfer function of each model determines how the input pulse is transformed in the output.
I've setup a simulation that inputs the same pulse into the three versions of our system model as shown in the schematic in Figure 5 and ran a few cases to demonstrate the problem with a few pulse durations of 1 ps, 10 ps, and 300 ps, each with 10 ps rise and fall times, which are defined, but not shown, in the SRC1 piece-wise linear voltage source.


The transient results in Figure 6 show that the ideal model and causal S-parameter model behave identically: we get an output that is the same as our input, but delayed by 123 ps. This is exactly what we would expect from a properly terminated, ideal transmission line. The output waveforms exhibit properties such as delay and shape preservation, and the magnitudes of the signals remain consistent with the input.
The non-causal S-parameter model behaves quite differently. Without the ideal case for reference, at first glance, it may not be obvious there's a problem. The output has roughly the same shape as the input, but with some ringing. Someone unfamiliar with the model's limitations might assume the ringing reflects imperfections in the physical system.
A closer look reveals the issue. The ringing begins as soon as the input pulse starts to rise, implying an instantaneous output response, which is physically impossible. More importantly, the rising edge of the output arrives with around 10 ps of delay.
Looking back at the S-parameter phase response, it's clear that the non-causal model is missing much of the phase information. The loss of phase fidelity is a key contributor to the erroneous, instantaneous-looking output. It's the phase response that encodes the system's delay and dispersion characteristics. Without accurate phase data, the reconstructed time-domain response cannot respect causality.
From my initial experiments with this setup, I originally extracted the non-causal S-parameter model to 20 GHz with 5 samples and got yet a different answer in the transient simulation has shown in Figure 7.

The 20 GHz non-causal model has more delay than the 35 GHz model and more ringing, and the output also begins to change as soon as the input changes. This further demonstrates that you don't know what you're going to get with an inaccurate model.
What About an "Almost" Causal Model?
After spending hours (or days) running a simulation or performing a complex measurement only to find that the resulting model fails the causality test by a single frequency point can be frustrating. Especially in a time crunch. It's tempting to ask: Is it really that bad? Can I still use the model anyway?
After some trial and error, I found that 99 linearly spaced points from 1 MHz to 35 GHz produced an S-parameter model that just barely failed the S-Parameter Toolkit's causality test at the lowest threshold setting of 0.01. However, all points passed when the threshold was relaxed to 0.02, so I’ll refer to this model as almost causal. The causality check assumes that any violation below the set threshold is negligible for practical purposes, so the choice of threshold directly affects whether a model is considered causal.
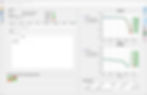
Figure 9 below shows the transient results with the ideal, causal, and almost causal models overlaid on one another to emphasize the match.

The output from the almost causal model shows minor ringing at the rising and falling edges. On the rising edge, there’s an overshoot of about 1.65% above the ideal model’s steady-state value (just under 1 V). This is a small discrepancy that likely wouldn’t impact most analyses, but it’s still measurable.
This is just one case, and we have the ideal model as a reference to assess the error. But when you're modeling an unknown system, how do you know the results are accurate? Or more realistically, accurate enough?
Here’s another interesting find: when I increase the sample count by just one — to 100 points — the model (which I’ll call the barely causal model) passes the causality test. But the resulting waveform is nearly identical to the almost causal version.
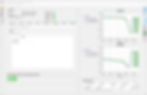

What does this tell us? Perhaps this model is technically causal — it passes at the 0.01 threshold — but it might not pass at a stricter threshold like 0.009. That raises the question: What does it really mean for a model to "pass" causality?
One takeaway here is that the causality test doesn’t just validate physics — it also gives us a practical measure of accuracy. A model that passes causality (at a reasonable threshold) likely contains enough frequency information to produce a trustworthy time-domain response.
What Does a Causality Test Actually Check?
When you test causality in ADS or another simulator, what is actually being checked?
At a high level, the goal is to verify whether the system violates physical causality. For S-parameter models, this check can be done in either the frequency or time domain, and different tools may use different methods.
Some simulators, including ADS, use frequency domain techniques based on the Kramers-Kronig relations. These relations connect the real and imaginary parts of the S-parameter response, making sure they're mathematically consistent with a causal system (which is why the S-Parameter Toolkit displays causality bounds on the real and imaginary plots across frequency). If the measured or simulated data doesn't obey these integral relations within tolerance, the system may exhibit non-physical behavior.
However, for practical insight (especially when visualizing the issue) we will explore the time-domain methods. One common approach is to convert the S-parameters to a time-domain impulse response using an inverse Fourier transform, then check whether any significant energy exists before time zero. The energy ratio (pre-t = 0 energy divided by total energy) becomes a practical metric to quantify causality violations.
This ratio is compared to a user-defined threshold, such as 0.01. If the ratio exceeds the threshold, the model is flagged as non-causal; if not, it's considered causal within acceptable bounds.
It's important to note that this isn't a strict pass/fail test. The Kramers-Kronig integrals yield bounds rather than exact values when applied to real-world data, which is discrete and bandwidth-limited. For ideal, continuous, and infinitely wideband input data, we'd get a definitive yes/no answer for causality. But in practice, we deal with finite data, so the test results reflect a range of acceptable values, not a binary outcome.
Some tools allow you to adjust the causality test threshold, which determines how much deviation from ideal behavior is tolerated. In time-domain-based methods, this might correspond to the ratio of energy before t=0 to total energy. In frequency domain methods, it often defines the tolerance band around the expected Kramers-Kronig constrained response. Either way, the threshold provides a way to balance numerical precision against practical usability.
This means the test is not binary. It’s a tradeoff between numerical sensitivity and practical accuracy — just like convergence tolerance in a simulator.
To illustrate this, I converted the through response (S21) of both the almost causal and causal models to the time domain using ADS's ts() function. This gives us an impulse-like view of the system's behavior — much like a TDR measurement (see our post on TDR measurements) — and allows us to compare the pre-t = 0 activity directly.

Although both responses show non-zero amplitude before t = 0 (which in this case is at 123 ps accounting for the line delay), the almost causal model has slightly more activity in this region as seen by the little bits of red behind the blue trace.
To quantify the difference, I calculated the energy ratio before t = 0 by summing the square of the normalized impulse response samples in that time window for each model's response (since energy is proportional to the integral of the squared magnitude over time). The almost causal model had 1.001x the pre-t = 0 energy of the causal model — meaning it contained about 0.1% more energy in the non-causal region.
Now suppose we'd like to reduce the ripple and total energy leading up to t = 0. There's only a 0.1% difference between using 99 samples and 1000. Adding more samples likely isn't going to add much improvement. But we know this converted time-domain impulse response is limited by the max frequency point in the dataset. Let's see what happens when we increase the max frequency and compare the conversions of two S-parameter datasets of 1000 linear samples, but with one out to 35 GHz and the other out to 350 GHz.

We've significantly decreased the pre-t = 0 ripple. The energy in the 35 GHz case is 5x more than the 350 GHz case.
So what's the takeaway here? Model your system to the highest frequency imaginable? Not necessarily. We've already seen that the 1000-sample, 35 GHz model is very accurate.
The takeaway is that it's not always about cranking up the sample count — after a certain point, increasing the number of frequency points yields diminishing returns. But bandwidth is a different story. The maximum frequency in your S-parameter dataset directly limits the time-domain resolution, especially near rapid transitions like t=0.
We saw that increasing the max frequency from 35 GHz to 350 GHz — while keeping the number of samples constant — significantly reduced pre-t = 0 ringing. This demonstrates that bandwidth, not just sample count, governs time-domain fidelity.
That doesn't mean you need to simulate to 350 GHz for every interconnect. The appropriate bandwidth depends on the sharpness of the transitions you want to model, not some arbitrary upper limit. If you're seeing spurious ringing or causality violations, it may not be a frequency point density issue. It may be a bandwidth issue. Make sure your model extends far enough in frequency to capture the transitions you care about.
Conclusion
Trustworthy time-domain simulation begins with a physically valid frequency-domain model — and that means it must be causal, or at least close enough to pass a meaningful causality check.
Even if the system you're modeling is inherently causal, you can still end up with a non-causal S-parameter model due to under-sampling, bandwidth limitations, or interpolation artifacts. And while a non-causal model might look reasonable, especially for small input signals or broad pulses, it can lead to inaccurate delay, artificial ringing, or even simulation instability in more sensitive applications.
The causality check isn't just a formality — it's a practical indicator of whether your model contains enough frequency content and continuity to accurately represent your system's behavior in the time domain.
If your model fails a causality check:
Increase the number of frequency points — if possible, focus additional points around the frequencies where violations were flagged
Extend the bandwidth — especially if your signals have fast edges
Follow solver-specific best practices for frequency sweep resolution
A model that passes a causality check is more likely to behave like the physical system it represents. A model that fails should raise some red flags.
That said, causality checks aren't binary. As we've shown, small violations isolated to a narrow frequency band may not meaningfully affect time-domain accuracy, especially in slower systems or broader pulses. The key is to understand the nature and magnitude of the violation before deciding to use or regenerate the model.
If you're building signal integrity and power integrity time-domain simulations that depend on high-fidelity results, verifying the causality of every model must be part of your workflow. It's one of those details that's far too often overlooked or taken for granted — until the results don't make sense.
At Signal Edge Solutions, we've seen firsthand how subtle modeling issues lead to costly debug time. We specialize in modeling high-speed interconnects (like UCIe), extracting broadband S-parameters and ensuring simulation fidelity through rigorous checks like causality, passivity, and reciprocity. We use efficient workflows (like test measurement automation) that ensure consistent results delivered on time.
Causality checks and frequency domain analysis not only validate your models but also help develop an intuitive understanding of system behavior and model accuracy, making debugging and design decisions more effective.
If you're developing time-domain simulations, you can't afford to second-guess. Let's talk. Reach out to us at info@signaledgesolutions.com and ask about our modeling and measurement services.
Acknowledgments
Special thanks to Jan Vanhese, the R&D Director at Keysight, for providing expert feedback during the writing of this post. His insight helped refine and clarify the explanation of the causality check, particularly regarding the use of Kramers-Kronig relations.
References
Eric Bogatin, Signal and Power Integrity – Simplified, 3rd ed., Pearson, 2018.
Keysight Technologies, Advanced Design System (ADS) Documentation, https://keysight.com
“How to Verify Signal Integrity Causality in S‑parameters,” Altium Resources, Altium Ltd, originally published August 11, 2020 by Jason J. Ellison
Verifying S-Parameter Data in the Keysight ADS Built-In Documentation


